Kumpulan Rumus Luas dan Volume Bangun Ruang + Contoh Soal Lengkap

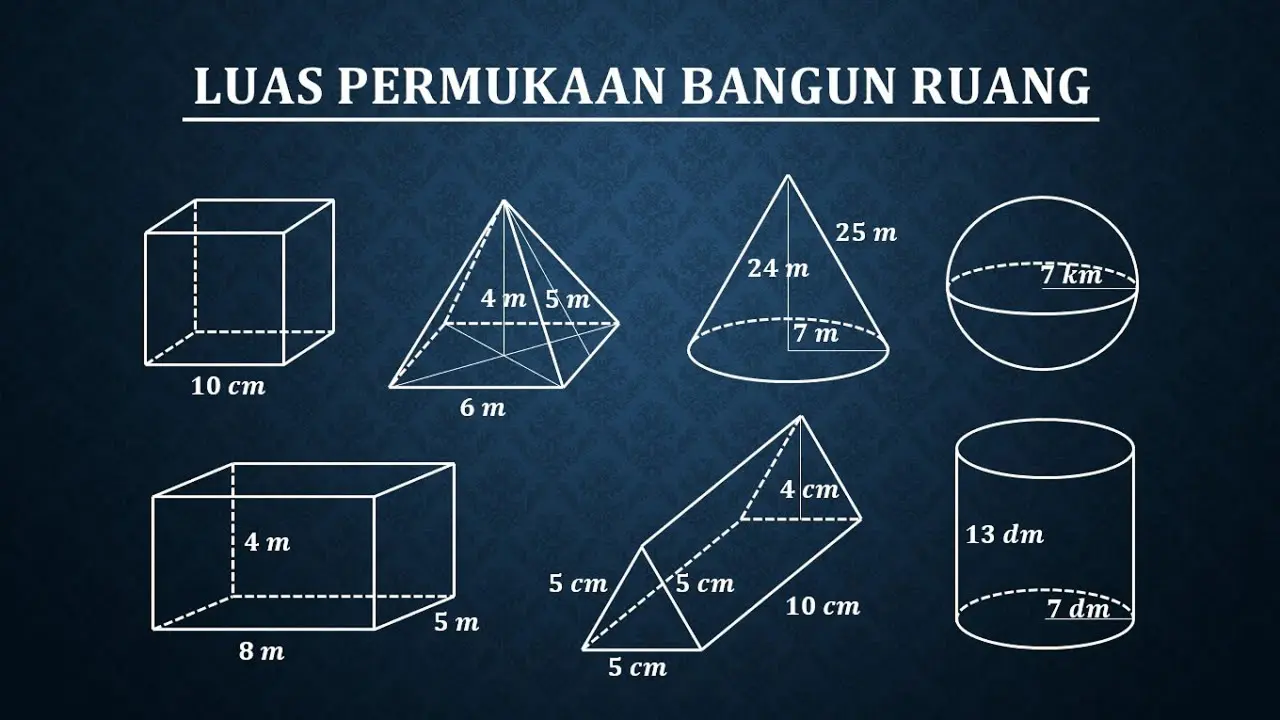
16 Juli 2025 – Menghitung volume bangun ruang seperti kubus, balok, dan bola adalah konsep penting dalam matematika. Melalui artikel ini, Anda akan mempelajari rumus luas dan volume bangun ruang dengan penjelasan yang mudah dimengerti, serta dilengkapi contoh soal untuk memperkuat pemahaman.

Bangun ruang adalah objek dalam matematika yang memiliki dimensi tiga—panjang, lebar, dan tinggi—sehingga dapat dihitung volumenya. Beberapa contoh bangun ruang yang umum termasuk kubus, balok, prisma, tabung, kerucut, dan bola. Dua hal yang sering dihitung dari bangun ruang adalah luas permukaan, yang merupakan total luas dari semua sisi, dan volume, yang mengindikasikan ruang yang ditempati oleh bangun tersebut.

Rumus untuk menghitung luas permukaan dan volume bervariasi tergantung pada jenis bangun ruang.

Untuk bangun kubus, luas permukaan dapat dihitung dengan rumus 6 × s², sedangkan volumenya menggunakan rumus s³, di mana s adalah panjang sisi kubus.
Sebagai contoh, jika sebuah kubus memiliki sisi sepanjang 4 cm, maka:

• Luas permukaan = 6 × 4² = 6 × 16 = 96 cm²

• Volume = 4³ = 64 cm³

Untuk bangun balok, luas permukaannya dihitung dengan rumus:
2 × (p × l + p × t + l × t)
Sementara volumenya dihitung dengan:
p × l × t,

Keterangan:
p = panjang, l = lebar, t = tinggi

Contoh soal:
Sebuah balok memiliki panjang 6 cm, lebar 4 cm, dan tinggi 3 cm. Hitunglah luas permukaannya!

Penyelesaian:
Luas permukaan balok = 2 × (p × l + p × t + l × t)
= 2 × (6 × 4 + 6 × 3 + 4 × 3)
= 2 × (24 + 18 + 12)
= 2 × 54
= 108 cm²

• Volume = 6 × 4 × 3 = 72 cm³

Untuk prisma, rumus luas permukaannya adalah:
(2 × luas alas) + (keliling alas × tinggi)
Sedangkan volumenya dihitung dengan:
luas alas × tinggi

Rumus ini berlaku untuk semua jenis prisma, baik prisma segitiga, segiempat, maupun bentuk lainnya, selama luas dan keliling alas diketahui.

Contoh lainnya adalah tabung.
Rumus luas permukaan tabung adalah:
2 × π × r × (r + t)
Sedangkan rumus volumenya:
π × r² × t,
di mana r adalah jari-jari alas dan t adalah tinggi tabung.

Contoh:
Jika sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm:

• Luas permukaan = 2 × π × 5 × (5 + 10) = 2 × π × 5 × 15 = 150π cm² ≈ 471,24 cm²

• Volume = π × 5² × 10 = π × 25 × 10 = 250π cm³ ≈ 785,40 cm³

Menguasai rumus-rumus ini sangat penting, terutama bagi siswa yang ingin memahami konsep matematika lebih dalam. Latihan dan pemahaman mengenai bangun-bangun tersebut dapat membantu meningkatkan kemampuan menghitung dan aplikasi dalam kehidupan sehari-hari.